Расчет статически неопределимых стержневых систем. Метод сил - расчет статически неопределимых рам

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ

КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра сопротивления материалов

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ШАРНИРНО–СТЕРЖНЕВЫХ СИСТЕМ ПРИ РАСТЯЖЕНИИ – СЖАТИИ

Методические указания по выполнению расчетно-графического задания по сопротивлению материалов для студентов всех специальностей

Составитель: В.Д. Моисеенко

Утверждены на заседании кафедры Протокол № 8 от 29.06.01

Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ

Кемерово 2002

Введение. Объем и цель задания

Статически-неопределимой шарнирно-стержневой системой называется такая, в которой усилия в стержнях и реакции в опорах нельзя определить только из условия равновесия.

На рис.1 показан обычный кронштейн, состоящий из двух стержней. Усилия N 1 и N 2 в стержнях этого кронштейна легко определяются из условия равновесия системы сходящихся сил, приложенных к вырезанному узлу С, так как два уравнения для этой системы сил с двумя неизвестными решаются.

Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 1,б), то усилия в стержнях прежним образом уже определены быть не могут, так как для узла С по-прежнему можно составить только два уравнения статического равновесия (ΣХ = 0; ΣY = 0), а число неизвестных усилий равно трем. Имеем один раз статически неопределимую систему.

Усложняя конструкцию и вводя новые стержни, можно получить два раза статически неопределимую систему (см. рис. 1,в), три раза и т.д. Следовательно, под n раз статически неопределимой системой понимается такая система, в которой число связей превышает число независимых уравнений статики на n единиц.

Необходимые для решения задачи дополнительные уравнения можно найти, рассматривая систему в деформированном состоянии и устанавливая связи между перемещениями и деформациями элементов конструкции. Полученные уравнения называются уравнениями совместимости деформаций.

На рис.2 приведены схемы некоторых статически неопределимых систем.

Рис.2. Некоторые виды статически неопределимых систем

При изучении раздела "Статически неопределимые стержневые системы" и выполнении данного расчетно-графического задания студент должен усвоить особенности статически неопределимых систем; получить навыки в раскрытии статической неопределимости, в определении усилий в элементах конструкций и подборе площадей поперечных сечений из условия прочности.

В задании студенту необходимо выполнить следующую работу:

- определить усилия в стержнях и подобрать площади поперечных сечений от действия внешних нагрузок;

- определить дополнительные напряжения в стержнях от изменения температуры;

- определить дополнительные монтажные напряжения, вызванные неточностью изготовления стержней;

- подобрать сечения стержней по предельному состоянию.

Объем и форма выполнения расчетно-графического задания зависят от объема изучаемого курса и оговариваются преподавателем на практических занятиях.

1. Краткие теоретические сведения

При решении статически неопределимых задач следует придерживаться следующего порядка:

1.1. Рассмотреть статическую сторону задачи. Построить план сил и составить уравнения статики.

1.2. Рассмотреть геометрическую сторону задачи. Построить план перемещений. Составить дополнительные уравнения совместимости деформаций в таком количестве, чтобы можно было найти все неизвестные усилия.

1.3. Рассмотреть физическую сторону задачи. По законам физики (при температурном расчете) и по закону Гука выразить деформации в уравнениях их совместимости через неизвестные усилия, действующие в стержнях:

	∆l t =α ∆t l		∆l N =
				EF .

1.4. Произвести совместное решение уравнений статики, геометрии, физики и определить неизвестные усилия.

1.5. Используя условия прочности при сжатии или растяжении N/F = [ σ ], произвести подбор площадей поперечных сечений стержней.

1.6. При известных усилиях в стержнях и принятых площадях поперечных сечений вычислить нормальные напряжения по формуле

σ = N F .

2. Пример

Дано: Абсолютно жесткая балка АВ опирается, как показано на рис.3, нагружена равномерно-распределенной нагрузкой и силой Р.

Рис.3. Схема статически неопределимой системы

Исходные данные для расчета

Материал

[σ ]Р ,

[ σ ] СЖ ,

α ,

F СТ

2 105

125 10-7

1 105

165 10-7

Требуется:

Определить усилия (N CТ ; N М ), площади поперечных сечений (F СТ ;

F М ) и напряжения (σ C р Т ;σ М р ) в стальном (СТ ) и медном (М ) стерж-

нях от действия внешних нагрузок Р и q .

;σ М t

Определить дополнительные напряжения в стержнях (σ СТ t

от изменения температуры на ∆ t = + 20 o C.

Определить дополнительные напряжения в стержнях, вызванные

неточностью изготовления вертикального стержня ∆ = 0,1 cм.

4. Определить суммарные напряжения в стержнях от действия нагрузок, изменения температуры и неточности изготовления.

2.1. Расчет статически неопределимой шарнирностержневой системы на внешнее нагружение

P = 30 кН q = 15 кН/м

А С В

Рис.4. Исходная расчетная схема

2.1.1. Статическая сторона задачи

Статическая сторона задачи рассматривается планом сил. План сил - это расчетная схема, на которой показаны все силы (и известные, и неизвестные), приложенные к элементу шарнирно-стержневой системы, равновесие которого рассматривается (в нашем случае это жесткая балка АВ). Разрежем стальной и медный стержни и отброшенные их нижние части заменим внутренними усилиями (рис. 5).

P = 30 кН q = 15 кН/м

А С В

60°

			а =2 м
N ст
						В = 4 м

Рис. 5. План сил от внешних нагрузок

Из плана сил (см. рис. 5) записываем уравнения статического равновесия. Для ответа на первый вопрос задачи необходимо знать усилия в стержнях - стальном и медном. Реакцию шарнирно-неподвижной опоры вычислять в данном случае нет необходимости. Поэтому из трёх

возможных уравнений статики (ΣX = 0; ΣY = 0 ; Σm c = 0 ) записываем

такое, в которое не входят реакции шарнирно-неподвижной опоры С:

∑ mC = 0

− N CТ a + q a 2 2 + p a + NM sin60o b = 0,

− N СТ 2 + 15 2 2 2 + 30 2 − NM 0,866 4 = 0,

После алгебраических действий уравнение равновесия примет вид

NCТ + 1,73NМ = 45.

2.1.2. Геометрическая сторона задачи

Геометрическая сторона задачи рассматривается планом перемещений. План перемещений - это расчётная схема, на которой показано положение шарнирно-стержневой системы до и после нагружения. На плане перемещений указываем перемещения точек балки (АА1 и ВВ1 ),

абсолютные деформации медного и стального стержней (∆ l СТ ; ∆ l М )

(рис. 6). Причём в силу малых деформаций точки балки перемещаем по вертикали вверх или вниз, а деформации наклонных стержней отмечаем перпендикуляром.

						60°
∆ l ст
						∆l м
			4 м

Рис. 6. План перемещений от действия внешних нагрузок

По плану перемещений составляем уравнение совместимости деформаций. В первую очередь запишем соотношение перемещений точек балки из подобия треугольников АА1 С и СВВ1 (рис. 6):

Перемещения точек балки (АА1 и ВВ1 ) выразим через деформации

	стержней (∆ l CТ ; ∆ l М ):
	АА1 = ∆ l СТ
	Из треугольника ВВ1 В2 выразим:
	BB =	B1 B2		∆l М
		sin60o		sin60o .

Выражения (2.3) и (2.4) подставим в соотношение (2.2):

∆ lCТ sin 60o
∆l М

		∆ lCТ 0,866
			∆l М
			0,866 ∆ lСТ =		0,5∆ lМ .
	Это и есть уравнение
			совместимости деформации.

2.1.3. Физическая сторона задачи

Полученное уравнение совместимости деформации (2.5) в таком виде не решается с уравнением равновесия (2.1), потому что входящие в них неизвестные величины разного характера.

Абсолютные деформации ∆ l CТ и ∆ l М в уравнении (2.5) выразим

через усилия в стержнях по закону Гука:

∆l =

N СТ l СТ

NМ lМ

E СТ F СТ

Е М F М

Подставим числовые значения исходных данных, а F СТ выразим

через F М согласно исходным данным:

F СТ

4 ,откуда F СТ = 4 F М = 0,75F М ,

NСТ 1,2

NМ 1,9

и получим

105 0,75 F

1 105 F

После выполнения арифметических действий получим:

0,67NСТ = 0,95NМ .

Получили уравнение совместимости деформаций, записанное через усилия в стержнях.

2.1.4. Синтез

Решим совместно уравнения равновесия (2.1) и уравнение совместимости деформаций (2.6).

NCТ + 1,73NМ = 45

0,67NСТ = 0,95NМ .

Из второго уравнения системы выразим усилие N СТ :

N СТ +		NМ = 1,42NМ

и подставим в первое уравнение системы.

	1,42 NМ +1,73 NМ = 45					3,15 NМ = 45,
		N М =		14,3 кН , тогда		NСТ = 1,42 14,3 = 20,3 кН.

Положительный результат N СТ и N М подтверждает наши предположения сжатия стального стержня и растяжения медного стержня, значит, усилия в стержнях будут:

NСТ = –20,3 кН;

NМ = 14,3 кН.

2.1.5. Подбор поперечных сечений стержней

Подбор поперечных сечений стержней ведется по условию прочности при растяжении – сжатии:

N F ≤ [ σ] .

а) Требуемая из условия прочности площадь поперечного сечения стального стержня будет определена:

N СТ

≥ 1,7 10− 4

[ σ СТ ] сж

F СТ

При этом согласно заданному отношению площадей

4 площадь

медного стержня должна быть равна:

4 1,7 10− 4

2,27 10− 4

б) Требуемая из условия прочности площадь поперечного сечения медного стержня будет определена:

					≥ 1,7 10	− 4 м 2
		[ σ М ] рас.		84 103

При этом, согласно заданному отношению площадей, площадь стального стержня должна быть равна:

FСТ = 4 3 FМ = 4 3 1,7 10− 4 = 1,275 10− 4 м2 ..

Принимаем большие площади поперечных сечений стержней:

FСТ = 1,7 10− 4 м2 ;

FМ = 2,27 10− 4 м2 .

При принятых площадях поперечных сечений медного и стального стержней определим напряжения в этих стержнях.

			N СТ			− 20,3 10− 3 МН		= − 119,4 МПа,
							1,7 10− 4 м2
			F СТ
		р N М					14,3 10− 3 МН	63 МПа.
	σМ =						2,27 10− 4 м2

2 .2. Температурный расчет статически неопределимой шарнирно-стержневой системы

Целью температурного расчета является определение дополнительных напряжений в медном и стальном стержнях от изменения температуры.

Допустим, система нагревается на ∆ t = 20 o C . Алгоритм решения остаётся прежним. Исходная расчетная схема представлена на рис. 7.

Для решения большинства статически неопределимых встречающихся на практике задач обозначенные приемы оказываются, однако, далеко не достаточными. Поэтому необходимо остановиться на более общих методах раскрытия статической неопределимости на примере стержневых систем.

Под стержневой системой в широком смысле слова понимается всякая конструкция, состоящая из элементов, имеющих форму бруса. Если элементы конструкции работают в основном на растяжение или сжатие, то стержневая система называется фермой (рис. 1).

Рис.1. Расчетная схема формы

Ферма состоит из прямых стержней, образующих треугольники. Для формы характерно приложение внешних сил в узлах.

Если элементы стержневой системы работают в основном на изгиб или кручение, то система называется рамой (рис. 2).

Особую, наиболее простую для исследования группу стержневых систем составляют плоские системы. У плоской рамы или фермы оси всех составляющих элементов до и после деформации расположены в одной плоскости. В этой же плоскости действуют все внешние силы, включая и реакции опор (см. рис. 2,а ).

Наряду с плоскими рассматриваются так называемые плоско-пространственные системы. Для такого рода систем оси составляющих элементов в недеформированном состоянии располагаются, как и для плоских систем, в одной плоскости. Внешние же силовые факторы действуют в плоскостях, перпендикулярных к этой плоскости (рис. 2,в) . Стержневые системы, не относящиеся к двум указанным классам, называются пространственными (рис.2,в ).

Рамы и фермы принято разделять на статически определимые и статически неопределимые . Под статически определимой понимается такая кинематически неизменяемая система, для которой все реакции опор могут быть определены при помощи уравнений равновесия, а затем при найденных опорных реакциях методом сечений могут быть найдены также и внутренние силовые факторы в любом поперечном сечении. Под статически неопределимой системой имеется в виду такая, опять же кинематически неизменяемая система, для которой определение внешних реакций и внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия.

а) плоская, б) плоскопространственная. в) пространственная

Рис.2. Расчетные схемы рамных конструкций:

Разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы, носит название степени или числа статической неопределимости . В зависимости от этого числа системы разделяются на один, два, три...., n раз статически неопределимые. Иногда говорят, что степень статической неопределимости равна числу дополнительных связей, наложенных на систему. Остановимся на этом вопросе подробнее.

Положение жесткого бруса в пространстве определяется шестью независимыми координатами, иначе говоря, жесткий брус обладает шестью степенями свободы. На брус могут быть наложены связи, т. е. ограничения, обусловливающие его определенное положение в пространстве. Наиболее простыми связями являются такие, при которых полностью исключается то или иное обобщенное перемещение для некоторых сечений бруса. Наложение одной связи снимает одну степень свободы с бруса как с жесткого целого. Следовательно, если на свободный жесткий брус наложено шесть связей, то положение его в пространстве как жесткого целого будет, за некоторыми исключениями, определено полностью и система из механизма, обладающего шестью степенями свободы, превращается в кинематически неизменяемую систему. То число связей, при котором достигается кинематическая неизменяемость, носит название необходимого числа связей . Всякую связь, наложенную сверх необходимых, называют дополнительной . Число дополнительных связей равно степени статической неопределимости системы.

Связи в рамах и стержневых системах делят обычно на связи внешние и связи внутренние, или взаимные. Под внешними связями понимаются условия, накладываемые на абсолютные перемещения некоторых точек системы.

а)внешняя связь, б) две внешние связи в) шесть внешних связей в общем случае

Рис.3. Схемы эквивалентных связей

Если, например, на левый конец бруса (рис. 3, а ) наложено условие, запрещающее вертикальное перемещение, говорят, что в этой точке имеется одна внешняя связь. Условно она изображается в виде двух шарниров или катка. Если запрещено как вертикальное, так и горизонтальное смещение, говорят, что наложены две внешние связи (рис. 3, б ). Заделка в плоской системе дает три внешние связи. Пространственная заделка соответствует шести внешним связям (рис. 3, б ). Внешние связи часто, как уже упоминалось, делят на необходимые и дополнительные. Например, на рис. 4, а и б показана плоская рама, имеющая в первом случае три внешние связи, а во втором - пять внешних связей. Для того чтобы определить положение рамы в плоскости как жесткого целого, необходимо наложение трех связей. Следовательно, в первом случае рама имеет необходимые внешние связи, а во втором, кроме того, две дополнительные внешние связи.

а) три внешних связи, б) пять внешних связей

Рис.4. Плоская рама

Под внутренними, или взаимными, связями понимаются ограничения, накладываемые на взаимные смещения элементов рамы. Здесь также можно говорить как о необходимых, так и о дополнительных связях. Так, например, плоская рама, показанная на рис. 5, а , имеет необходимое количество как внешних, так и внутренних связей между элементами. Это - кинематически неизменяемая система. Если будут заданы внешние силы, мы сможем найти как реакции опор, так и внутренние силовые факторы в любом поперечном сечении рамы. В той же раме, показанной на рис. 5, б , дополнительно наложены две дополнительные внутренние связи, запрещающие взаимное вертикальное и горизонтальное смещения точек А и В . Система в данном случае дважды статически неопределима (иногда добавляют: «внутренним образом»).

В раме рис. 4, а и б также имеются внутренние дополнительные связи. Контур рамы полностью замкнут. Разрезая его в любом сечении (рис.5 в), мы, не нарушая кинематической неизменяемости, получаем возможность при заданных силах найти внутренние силовые факторы в каждом сечении рамы. Следовательно, разрезая замкнутую раму, мы снимаем дополнительные связи, т.е. позволяем сечениям А и В поворачиваться и смещаться в двух направлениях друг относительно друга. Обобщая, можно сказать, что замкнутый плоский контур имеет три дополнительные взаимные связи- трижды статически неопределим. Таким образом, рама, показанная на рис. 4, а , трижды статически неопределима. Рама, показанная на рис. 4, б , пять раз статически неопределима (три раза внутренним образом и два раза - внешним).

а) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей

Рис.5. Классификационные признаки рам:

Рассмотрим теперь несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 6 показано несколько рам. Последовательно рассмотрим их.

а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.

б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира (рис. 7). Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти - три раза статически неопределимой.

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.

а) статически неопределимая - семь, б) - три, в) - четыре, г) - три, е) - двенадцать,
ж) - семь, д) - три, и) - тринадцать раз статически неопределима

Рис.6. Примеры рамных конструкций:

в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т. е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.

г) Рама три раза статически неопределима.

д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это - механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

Рис.7. модель двух совпадших шарниров

е) Рама - пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур) Система 12 раз статически неопределима.

ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз - внутренним).

з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.

и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 6, и ). Система 30 раз статически неопределима.

Лекция № 38. Метод сил.

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил . Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.

Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы .

а-д) модификации основной системы
Рис.1. пример стержневой рамы:

Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а ), б ),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,- с другой.

Рис.2. Некорректные преобразования заданной системы в основные по причине кинематической изменяемости- а) б), или статической определимости во всех узлах - в)

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X i -, где i - номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X i , - являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

а)-д) по отношению к заданной системе
Рис.3. Пять разновидностей основных систем

Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы . На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.

Теперь остается составить уравнения для определения неизвестных.

Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.

Перейдем теперь к составлению уравнений для определения неизвестных силовых факторов. Условимся через обозначать взаимное смещение точек системы.

Рис.4. Пример расчета рамы а)по выбранной основной системе- б)

Первый индекс при соответствует направлению перемещения, а второй - силе, вызвавшей это перемещение.

В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:

Индекс 1 означает, что речь идет о перемещении по направлению силы Х 1 , а индекс [Х 1 , Х 2 ,..., Р ] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать:

Так как под величиной понимается взаимное смещение точек, то обозначает вертикальное смещение точки В относительно С , - горизонтальное взаимное смещение тех же точек, есть взаимное угловое смещение сечений В и С . Угловым смещением будет также в рассматриваемой системе величина .

В точках A и D смещения являются абсолютными. Но абсолютные смещения можно рассматривать как смещения, взаимные с неподвижными отброшенными опорами. Поэтому принятые обозначения приемлемы для всех сечений системы.

Пользуясь принципом независимости действия сил, раскроем выражения для перемещений

Аналогичным образом запишем и остальные пять уравнений: каждое из слагаемых , входящих в уравнение, обозначает перемещение в направлении силы с первым индексом под действием силы, стоящей во втором индексе. Поскольку каждое перемещение пропорционально соответствующей силе, величину можно записать в следующем виде:

Что касается перемещений , и т. д., то под индексом Р будем понимать не просто внешнюю силу Р , а вообще систему внешних сил, которая может быть произвольной Поэтому величины , ,... в уравнениях оставим неизменными.

Теперь уравнения примут вид:

Эти уравнения являются окончательными и носят название канонических уравнений метода сил . Число их равно степени статической неопределимости системы. В некоторых случаях, как увидим далее, когда имеется возможность сразу указать значения некоторых неизвестных, число совместно решаемых уравнений снижается. Остается теперь выяснить, что представляют собой коэффициенты и как следует их определять. Для этого обратимся к выражению (6.1).

Если , то

Следовательно, коэффициент это есть перемещение по направлению i -го силового фактора под действием единичного фактора, заменяющего k -й фактор. Например, коэффициент уравнения представляет собой взаимное горизонтальное смещение точек B и С , которое возникло бы в раме, если бы к ней вместо всех сил была приложена только единичная сила в точке А (рис. 5 а). Если, например, вместо сил приложив единичные силы, а все прочие силы с эквивалентной системы снять (рис. 5 б), то угол поворота в сечении D под действием этих сил будет , горизонтальное перемещение в точке А будет и т. д.

а) , б) и
Рис.5. Интерпретация коэффициентов уравнений метода сил:

Весьма существенно отметить, что в проделанном выводе совершенно не обусловливается то, каким образом возникают перемещения . Хотя мы и рассматриваем раму, работающую на изгиб, все сказанное с равным успехом может быть отнесено, вообще, к любой системе, работающей на кручение, растяжение и изгиб или на то, другое и третье совместно.

Обратимся к интегралам Мора. Для того чтобы определить величину , следует вместо внешних сил рассматривать единичную силу, заменяющую k -й фактор. Поэтому внутренние моменты и силы , , , , и в интегралах Мора заменим на , , , , и , понимая под ними внутренние моменты и силы от единичного k -го фактора. В итоге получим:

где , … - внутренние моменты и силы, возникающие под действием i -го единичного фактора. Таким образом, коэффициенты получаются как результат перемножения i -го и k -го внутренних единичных силовых факторов. Индексы i и k непосредственно указывают, какие факторы должны быть перемножены под знаком интегралов Мора. Если рама состоит из прямых участков и можно пользоваться правилом Верещагина, то представляет собой результат перемножения i -х единичных эпюр на k -е единичные эпюры.

Очевидно, что

Это следует, с одной стороны, непосредственно из выражений для , а с другой стороны, из теоремы о взаимности перемещений, поскольку перемещения и возникают под действием одной и той же силы, равной единице.

Величины , входящие в канонические уравнения, представляют собой перемещения в направлениях 1, 2,..., возникающие под действием заданных внешних сил в эквивалентной системе. Они определяются перемножением эпюры моментов заданных сил на соответствующие единичные эпюры.

Пример Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 6.

Рис.6. Заданная расчетная схема

Рама три раза статически неопределима. Выбираем основную систему, отбрасывая левую заделку. Действие заделки заменяем двумя силами , и моментом и определяем эквивалентную систему (рис. 7).

Рис.7. Динамика решения: от эквивалентной системы и силовой эпюры Р , включая эпюры моментов от единичных сил: 1, 2, 3 в точках приложения неизвестных , ,

Канонические уравнения (6.2) принимают для рассматриваемой системы такой вид:

Основные перемещения в рассматриваемой раме определяются изгибом. Поэтому, пренебрегая сдвигом и сжатием стержней, строим эпюры изгибающих моментов от заданной силы P и от трех единичных силовых факторов (рис. 7).

Определяем коэффициенты уравнений, считая, что жесткость на изгиб всех участков рамы постоянна и равна EJ . Величина определяется перемножением первой единичной эпюры самой на себя. Для каждого участка берется, следовательно, площадь эпюры и умножается на ординату этой же эпюры, проходящую через ее центр тяжести:

Заметим, что величины при всегда положительны, поскольку площади эпюр и ординаты имеют общий знак.

, , , , , , , .

Подставляем найденные коэффициенты в канонические уравнения. После сокращений получаем:

, ,

Решая эти уравнения, находим:

Раскрытие статической неопределимости на этом заканчивается.

Рис.8. Суммарная эпюра изгибающих моментов.

Эпюра изгибающих моментов может быть получена наложением на эпюру моментов заданных сил трех единичных эпюр, увеличенных соответственно в , и раза Суммарная эпюра изгибающих моментов представлена на рис. 8. Там же пунктиром показана форма изогнутой оси рамы.

Лекция № 39. Расчет толстостенных цилиндров.

В тонкостенных цилиндрических резервуарах, подвергнутых внутреннему давлению, вполне возможно при вычислениях считать напряжения равномерно распределенными по толщине стенки. Это допущение мало отзывается на точности расчета.

В цилиндрах, у которых толщина стенок не мала по сравнению с радиусом, подобное предположение повело бы к большим погрешностям. Расчет таких цилиндров дан Ляме и Гадолиным в 1852 - 1854 гг. Работы русского академика А. В. Гадолина в области расчета кривых стержней в применении к расчету прочности артиллерийских орудий создали ему мировую известность. Отечественные артиллерийские заводы (и многие зарубежные) до сих пор проектируют и изготовляют орудия, пользуясь исследованиями Гадолина.

На Рис.1 изображено поперечное сечение толстостенного цилиндра с наружным радиусом , внутренним ; цилиндр подвергнут наружному и внутреннему давлению .

Рис.1. Расчетная схема толстостенного цилиндра.

Рассмотрим очень узкое кольцо материала радиусом внутри стенки цилиндра. Толщину кольца обозначим . Пусть АВ изображает небольшую часть этого кольца, соответствующую центральному углу .

Размер выделенного элемента, перпендикулярный к плоскости чертежа, возьмем равным единице. Пусть и будут напряжения, действующие по внутренней и наружной поверхностям элемента АВ , a - напряжения по его боковым граням. По симметрии сечения цилиндра и действующей нагрузки элемент АВ перекашиваться не будет, и касательные напряжения по его граням будут отсутствовать. По граням элемента AB , совпадающим с плоскостью чертежа, будет действовать третье главное напряжение , вызванное давлением на днище цилиндра. Это напряжение можно считать постоянным по всем точкам поперечного сечения цилиндра.

(1)

Условие равновесия дало только одно уравнение для нахождения двух неизвестных напряжений. Задача статически неопределима, и необходимо обратиться к рассмотрению деформаций. Деформация цилиндра будет заключаться в его удлинении и в радиальном, перемещении всех точек его поперечных сечений. Назовем радиальное перемещение точек внутренней поверхности рассматриваемого элемента через u (Рис.3). Точки наружной поверхности переместятся по радиусу на другую величину ; таким образом, толщина dr выделенного элемента увеличится на du , и относительное удлинение материала в радиальном направлении будет

R и подставим в него значение и и то прочность цилиндра определяется этими последними. Применяя третью теорию прочности (наибольших касательных напряжений), получаем, что наибольшая разность главных напряжений, равная (для случая )

(11)

Рис.3. Распределение напряжений по толщине цилиндра при

будет иметь место в точках внутренней поверхности цилиндра и всегда будет по абсолютной величине значительно больше внутреннего давления.

Общие сведения

Расчет статически неопределимых систем методом сил начинают с вы­явления степени статической неопределимости. Степень статической не­определимости любой системы может быть установлена по формуле, которая для выявления степени статической неопределимости рам будет иметь вид:

Л = 3К - Ш, (23)

где Л – число лишних связей, К – число контуров, а для неразрезных балок - формулой (24):

Л = С оп - 3, (24)

где С оп - число опорных стержней.

Остановимся на применении формулы (23).

Пример 7.1.

Пользуясь формулой (23), опреде­лить степень статической неопределимости рамы, изображенной на рис. 7.1.

Рис. 7.1. Рама

Решение

Рама состоит из двух замкнутых контуров I и II. Шарнирно-неподвижная опора А равноценна одному простому шарниру, шарнирно-подвижная опора В - двум шарнирам. Следова­тельно, Ш= 1 + 2 = 3.

Степень статической неопределимости Л = 3К - Ш=3∙2 - 3 ==3 - рама трижды ста­тически неопределима.

Пример 7.2.

Определить степень статической неопределимости рамы, приведенной на рис. 7.2.

Рис. 7.2. 3-х контурная рама. Рис. 7.3. 6-ти контурная рама

Решение

Рама имеет три замкнутых контура (I, II и III). Сум­марное число шарниров Ш = 6 (два простых шарнира - Е и F и две шарнирно подвижные опоры -A и D). Число лишних связей Л =3∙3 - 6=3. Следовательно, рама трижды статически неопределима.

Пример 7.3.

Определить степень статической неопределимости рамы, изображённой на рис. 7.3.

Решение

В этой раме шесть замкнутых контуров. Простых шар­ниров - три (шарниры F,H и I ). Шарнир G - двукратный, как соединяю­щий три стержня. Каждая из шарнирно-подвижных опор А, В, D и Е эквивалентна двум простым шарнирам, а шарнирно-неподвижная опора С - одному. Следовательно, Ш = 1∙3 + 2∙1 + 2∙4 + 1 =14. Тогда степень статической неопределимости Л =3∙6-14 =4. Таким образом, рама имеет четыре лишние связи, т. е. является четырежды статически неопределимой.

После того как будет установлена степень статической неопределимости, выбирают основную систему.

Выбор основной системы

Основной системой будем называть геометрически неизме­няемую статически определимую систему, полученную из заданной стати­чески неопределимой путем устранения лишних связей и нагрузки.

На рис. 7.4., а показана статически неопределимая рама - заданная система. Степень статической неопределимости этой системы:

Л = 3К - Ш =3∙1-0 =3.

Следовательно, чтобы из заданной системы получить основную систему, надо освободить раму от нагрузки q и отбросить три лишние связи; по­следнее может быть выполнено различными способами, но в результате применения любого из них полученная основная система должна быть геометрически неизменяемой.

Так, например, на рис. 7.4., б показана основная система, полученная путем устранения нагрузки q и правой защемляющей опоры В, эквивалент­ной трем лишним связям.

Рис. 7.4. Выбор основной системы

Теперь сечение В основной системы может перемещаться по горизонталь­ному и вертикальному направлениям и поворачиваться в плоскости рамы на некоторый угол, т. е. в основной системе стали возможными те перемещения, которым в заданной системе препятствует правая защемляющая опора.

Чтобы устранить различие между заданной и основной системами, поступим так, как показано на рис. 7.4., в: нагрузим основную систему заданной нагрузкой q и вточке В ее, по направлениям указанных переме­щений сечения В, приложим соответствующие им пока неизвестные, горизонтальную и вертикальную силы Х 1 ; Х 2 и момент Х 3 .

Величины Х 1 ; Х 2 ; X 3 называются лишними неизвестными и являются искомыми реакциями лишних связей, заменяющими действие отброшен­ных лишних связей на заданную систему.

Обращаем внимание, на то, что основная система, нагружен­ная заданной нагрузкой и лишними неизвестными, в отношении внут­ренних усилий и перемещений эквивалентна заданной статически неопре­делимой.

Кроме того, условимся в дальнейшем, как это принято в практических расчетах, основную систему на отдельном рисунке не изображать и взамен ее приводить рисунок выбранной основной системы, нагруженной задан­ной нагрузкой и лишними неизвестными.

Далее составляют уравнения совместности перемещений, каждое из которых должно выражать условие равенства нулю суммарного пере­мещения по направлению той или иной, отброшенной связи (неизвестной силы) от заданной нагрузки и всех лишних неизвестных. Эти уравнения, написанные в определенной, раз навсегда установленной форме, называют каноническими уравнениями метода сил. Число их должно равняться числу отброшенных связей. Для рассматриваемой рамы необходимо составить, таким образом, три канонических уравнения, имеющих следующий вид:

δ 11 X 1 + δ 12 X 2 + δ 13 X 3 + ∆ 1 p = 0

δ 21 X 1 + δ 22 X 2 + δ 23 X 3 + ∆ 2 p = 0 (25)

δ 31 X 1 + δ 32 X 2 + δ 33 X 3 + ∆ 3 p = 0

Где δ 11 -перемещение точки приложения силы X 1 по направлению этой силы от единичной силы = 1;

δ 11 X 1 -перемещение той же точки в том же направлении, вызванное полным значением X 1 ;

δ 12 - перемещение точки приложения силы X 1 по направлению этой силы, вызванное единич­ной силой

δ 12 X 2 - перемещение той же точки в том же направле­нии, вызванное полным значением силы Х 2 ;

δ 13 - перемещение точки приложения силы Х х по направлению этой силы от единичной силы = 1;

δ 13 X 3 - перемещение той же точки в том же направлении, вызван­ное полным значением силы Х 3 ;

∆ 1 p -перемещение той же точки в том же направлении, вызванное заданной нагрузкой; δ 21 X 1 - перемещение точки приложения силы Х 2 по направлению этой силы, вызванное силой X 1 , и т. д.

Следует иметь в виду, что один раз составленные в общем виде п канонических уравнений с п неизвестными применимы для любой п раз стати­чески неопределимой системы. Так, уравнения (25) справедливы для любой трижды статически неопределимой системы.

Составив канонические уравнения метода сил, следует перейти к вы­числению единичных δ ik и грузовых ∆ ip перемещений.

Для этого предварительно введем понятия о грузовом и единичном состояниях основной системы.

Грузовым назовем то состояние основной системы, при котором она находится только под действием заданной нагрузки.

Единичным будем называть состояние основной системы, при ко­тором она нагружена только одной силой, равной единице е = 1, дейст­вующей в направлении неизвестной реакции X t .

Заметим, что число единичных состояний основной системы должно соответствовать степени статической неопределимости заданной системы,

т. е. числу лишних неизвестных. Изобразив на рисунках грузовое и отдельно все единичные состояния основной системы, строят соответствующие им грузовую М р и единичные M 1 , M 2 , ..., М п эпюры изгибающих моментов.

Наконец, используя способ перемножения эпюр, вычисляют единич­ные δ ik и грузовые ∆ ip перемещения.

Перемножая эпюры, следует помнить, что на основании теоремы о взаимности пере­мещений (теоремы Максвелла) единичные перемещения с взаимно пере­ставленными индексами равны между собой, т. е. δ ik = δ ki .

Вычисленные значения δ ik и ∆ ip подставляют в канонические уравнения и решают полученную систему уравнений, в результате чего нахо­дят значения неизвестных реакций связей X 1 , X 2 , ..., Х п.

Нагрузив те­перь основную систему заданной нагрузкой и уже известными силами X 1 = А 1 ;Х 2 = А 2 , ..., Х п = А п, строят обычным путем (как для статиче­ски определимой системы) эпюры Q, М и N, которые и являются оконча­тельными эпюрами поперечных сил, изгибающих моментов и продольных сил для заданной системы.

Окончательную эпюру изгибающих моментов можно также получить путем суммирования ординат эпюры М р с соответствующими ординатами эпюры

После определения неизвестных можно сразу получить эпюру М, по которой построить эпюру Q, а продольные силы определить из условий равновесия вырезаемых узлов рамы. Опорные реакции в этом случае находят в последнюю очередь, используя эпюры Q, М и N,

Умноженными на X 1 , ординатами эпюры , умноженными на Х 2 ..., и ординатами эпюры , умноженными на Х п, т. е.

Единичные перемещения с одинаковыми индексами (δ 11 , δ 22 , δ 33 и т.д.) принято называть главными перемещениями , а с разными индексами

(δ 12 , δ 13 , δ 23 и т.д.) - побочными .

Главные перемещения никогда не обращаются в нуль и всегда имеют положительное значение, так как в этом случае эпюры умножаются сами на себя, т. е. и площадь ω и ордината у берутся из одной и той же эпюры.

Побочные перемещения могут быть положительными, отрицательными, а при удачном выборе основной системы и равными нулю. В последнем случае в значительной мере сокращаются и упрощаются операции по вы­числению перемещений.

На рис. 7.4., б основная система выбрана неудачно, так как для нее ни одно из побочных перемещений не обратится в нуль. Ниже эта рама будет рассчитана, при более рациональном выборе основной системы.

Статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые , так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчета статически неопределимых систем являются:

1. Метод сил . Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

Канонические уравнения метода сил

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой , однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. - это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; - перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде:

где - единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил :

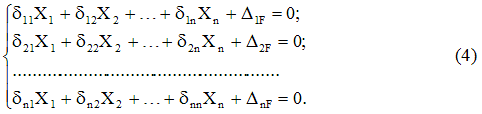
Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил :

1. Определить степень статической неопределимости .
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений .
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

Выбор основной системы

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил .

Вычисление коэффициентов и свободных членов канонических уравнений

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

Универсальная проверка коэффициентов и свободных членов канонических уравнений

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру - эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

Перемножим суммарную единичную эпюру с эпюрой :

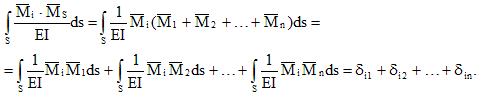
Таким образом результат перемножения суммарной и i-ой единичной эпюр - это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия.

Для того чтобы стержневые системы (балки, рамы и т. п.) могли служить сооружениями и выдерживать внешние нагрузки, необходимо наложить на них определенные связи, которые делят на связи внешние и внутренние. Под связью обычно понимают тела (препятствия), ограничивающие перемещение другим телам, точкам или сечениям конструкции. На практике такие тела называют опорными устройствами, фундаментами и т. п. В инженерных расчетах вводится понятие идеальных связей. Если, например, на левый торец бруса (рис. 1.1, а) наложено условие, запрещающее вертикальное перемещение, то говорят, что в этой точке имеется одна внешняя связь. Условно она изображается в виде стержня с двумя шарнирами. Если запрещено вертикальное и горизонтальное смещения, то на систему наложены две внешние связи (рис. 1.1, б). Заделка в плоской системе дает три внешние связи (рис 1.1, в), препятствующие вертикальному, горизонтальному смещениям и повороту сечения заделки. лд Рис. 1.1 Для того чтобы закрепить тело (стержень) на плоскости и обеспечить ему геометрическую неизменяемость, необходимо и достаточно наложить на него три связи (рис. 1.2), причем все три связи не должны быть взаимно параллельными и не должны пересекаться в одной точке. В дальнейшем связи, обеспечивающие геометрическую неизменяемость системы и ее статическую определимость, будем понимать как необходимые связи. Геометрически неизменяемой системой называют такую систему, которая может изменять свою форму только за счет деформации ее элементов (рис. 1.2), в то время как геометрически изменяемая система может допускать перемещения и при отсутствии деформации (рис. 1.3). Такая система является механизмом (рис. 1.3, а). 5 Рис. 1.2 Наряду с отмеченными различают еще мгновенно изменяемые системы, под которыми понимают системы, допускающие бесконечно малые перемещения без деформации ее элементов (рис. 1.4). Рис. 1.3 Так, например, под действием силы P, приложенной в шарнире Д (рис. 1.4, а), стержни ДВ и ДС без деформации повернутся относительно шарниров В и С на бесконечно малый угол d . Тогда из условия равновесия, вырезанного при малом значении величины силы P усилия в стержнях ДВ и ДС будут стремиться к бесконечности, вызывая осевую деформацию стержней и изменяя положение системы. 6 Рис. 1.4 Для рамы на рис. 1.4, б при рассмотрении уравнения статики момент силы P не уравновешивается (реакция R1 ,не может вызывать момента относительно рассматриваемой точки, так как линия ее действия проходит через эту точку). Аналогичная особенность проявляется и для системы, показанной на рис. 1.4, в. Момент силы P относительно точки k не уравновешивается. Таким образом, эти системы также допускают бесконечно малые перемещения (относительно моментной точки) без деформации их элементов. В сооружениях и конструкциях такие системы недопустимы. Если геометрически неизменяемая система имеет помимо необходимых еще и дополнительные связи, то независимых уравнений статики оказывается недостаточно для определения неизвестных усилий (реакций связей) и такая система называется статически неопределимой. Разница между числом неизвестных усилий, подлежащих определению, и числом независимых уравнений статики характеризует степень статической неопределимости, которую принято обозначать символом n . Так, балка и рама, представленные на рис. 1.5, являются два раза (дважды) статически неопределимыми. В этих схемах число неизвестных реакций равно пяти, а число независимых уравнений статики, которые можно составить для каждой из них, равно трем. Всякий замкнутый контур представляет собой систему трижды статически неопределимую (рис. 1.6). Рис. 1.6 Постановка одиночного шарнира снижает степень статической неопределимости системы на единицу (рис. 1.7, а), поскольку изгибающий момент в шарнире отсутствует. Под одиночным шарниром понимают шарнир, соединяющий концы двух стержней. Рис. 1.7 Шарнир, включенный в узел, где сходятся концы нескольких стержней, понижает степень статической неопределимости системы на число одиночных шарниров, определяемых по формуле О=С–1. Здесь под C понимают число стержней, сходящихся в узле. Например, в раме (рис. 1.7, б) число одиночных шарниров О=С–1=3-1=2, поэтому степень статической неопределимости понижается на две единицы и становится равной n4 .

Расчет статически определимых рам

Основные понятия Рамой называют стержневую систему, у которой все или некоторые узловые соединения являются жёсткими (рис. 1.8 а). Жёсткий узел характеризуется тем, что угол между осями стержней, которые его образуют, не изменяется при действии нагрузки (рис. 1.8 а). Угол между касательными к упругим линиям ригеля и наклонной стойки в узле В сохраняет неизменную величину α, а угол между касательными к упругим линиям того же ригеля и правой стойки в узле D сохраняет неизменную величину β. Рамы могут быть плоскими, когда все оси стержней лежат в одной плоскости (рис 1.8 а, б, в) и пространственными (рис. 1.8 г). Горизонтальный стержень рамы называют ригелем, а стержни, его поддерживающие, называют стойка. Левая стойка наклонная, а правая вертикальная. Рамы могут быть простыми, состоящими из трёх стержней (рис 1.8), сложными, многопролётными (рис 1.8 б) и многоярусными (рис 1.8 в). Также они подразделяются на статически определимые (рис 1.8 б), когда число неизвестных реакций, усилий меньше или равно числу независимых уравнений статики, которые могут быть составлены для данной рамы, и статически неопределимые, если это условие не выполняется (рис 1.8 а, в, г), об этом будет сказано далее. В отличии от балок, в сечениях рам, наряду с изгибающими моментами, поперечной силой, возникает еще и продольная сила. Рис. 1.8 Определение усилий (М, Q, N) выполняются также, как и в балках посредством метода сечений (РОЗУ). При этом правило знаков для изгибающего момента М и поперечной силы Q такое же, как для балок, а для продольной силы N, как в 9 стержнях при растяжении – сжатии. Определение нормальных n и касательных напряжений производится по тем же зависимостям, как в балках, если стержень испытывает изгиб. В случае сложного сопротивления, когда наряду с изгибающим моментом возникает в стержне еще и продольная сила, то расчет ведется как и при изгибе с растяжением – сжатием, излагаемым в разделе "Сложное сопртивление”. Пример 1.1 Для заданной рамы (рис.1.9) построить эпюры внутренних усилий и найти величину и направление полного перемещения сечения К, если Р = 5кН; q = 10 кН/м; EIz = const; сечения стоек и ригеля одинаковые I = 8000 см4: 1. Находим реакции опор: а) вертикальные реакции V1,V2: б) горизонтальные реакции Н1 и Н2: 2. Строим эпюры внутренних усилий М, Q, N. а. Построение эпюры изгибающих моментов М.

Расчет статически неопределимых стержневых систем методом сил

Выбираем точку наблюдения, считая, что она находится внутри контура. В этом случае поля расположены выше участков 1-3, 3-4, 4-К, 4-2, рассматриваются как внешние, а внутри контура – внутренние. При определении изгибающих моментов придерживаемся так же правил, что и в балках. Вычисляем моменты в характерных сечениях каждого из участков рамы. Участок 1-3. Момент на конце со стороны опоры – 1, М13 = 0. Момент в узле 3, Знак минус потому, что на участке 1-3 нижняя отсеченная часть изгибается выпуклостью вверх по отношению к наблюдателю. Участок 3-4 (ригель). Момент в начале участка (в сечении узла 3) М34 , такой же, как и на стойке 1– Момент В шарнире момент равен нулю. Участок 2-4 (наклонная стойка) Участок 4-К В начале участка момент МК4 = 0. В конце участка Эпюра изгибающих моментов показана на (рис. 1.10, а) 11 Рис. 1.10 Выполняем проверку правильности построения эпюры М. Если эпюра М построена верно, то любой внеопорный узел или любая часть рамы под действием внешних и внутренних сил должна находиться в равновесии. Вырежем из рамы сечениями бесконечно близкими к узлу, например, узел (4) и рассмотрим его равновесие. Значения моментов берем в соответствующих сечениях из эпюры М (рис. 1.10, б). Уравнения моментов узла (4) имеет вид

Особенности расчета методом сил многопролетных неразрезных балок

Условие выполняется, значит в примыкающих к узлу (4) сечениях моменты определены верно. Аналогично выполняется проверка в узле (3) и т. д. Примечание Если в узле приложены сосредоточенные внешние усилия (момент или силы) то они должны быть учтены при проверке. Распределенная нагрузка не показывается, т. к. dx – малая величина. б. Построение эпюры поперечных сил Q. Придерживаемся того же правила знака, как для балок: если равнодействующая внешних сил слева от сечения направлена вверх, а справа вниз поперечная сила Q > 0, если наоборот – т Участок 1–3. При рассмотрении левой отсеченной части 10 кН.(минус потому, что левая отсеченная часть находится под воздействием силы Н1 12 направленной вниз, если смотреть на отсеченную часть из точки наблюдателя). Поперечная сила постоянна по длине этого участка (рис. 1.11, а) Рис. 1.11 Участок 3-4 Поперечная сила в любом сечении, взятом на расстоянии х от узла (3) при рассмотрении сил действующих от сечения слева, равна 103 01QV xqx. При х = 0, получим поперечную силу в сечении левее узла (3), т. е. Q34 30кН; при х = 3 м, получаем поперечную силу Q, т. е. в сечении левее узла (4). Поперечная сила на участке 3–4 изменяется по линейному закону (рис.1.11, а). Участок 4–К. В сечении на расстоянии х от правого конца участка (рис. 1.11, а) поперечная сила равна (линейный закон). При х = 0, получаем, а при х = 3 м, получаем Участок 2–4. Поперечную силу в сечении этого участка получим, проектируя внешние силы Н2, V2, приложенные в точке 2 (рис. 1.11,а) на ось У, перпендикулярную продольной оси стержня. По длине участка 3–4 поперечная сила постоянная. Эпюра поперечных сил изображена на (рис. 1.11, а).

Использование свойств симметрии при раскрытии статической неопределимости стержневых систем

в. Построение эпюры продольных сил N. Вычисляем продольную силу в сечении каждого участка. Участок 1–3. Рассматриваем нижнюю часть (рис. 1.12) Минус взят потому, что продольная сила, уравновешивающая реакцию V1, направлена к сечению, т. е. навстречу реакции V1, значит отсеченный участок испытывает сжатие. Если бы продольная сила была направлена от сечения, то знак N – положителен. Участок 3-4 (на ригеле). Продольная сила N30 кН, отрицательна, так как сжимающая. В сечении х (рис.1.12, б) на участке 4-К: перпендикулярны продольной оси участка. Участок 2–4. Рис. 1.12 На наклонной стойке в сечении х продольную силу находим, проектируя внешние силы V2 и Н2 на ось Х, совпадающею с осью стержня (рис. 1.12): 34 5 4 (сжатие), Поэтому присваиваем знак минус N24 кН. 14 Эпюра продольных сил изображена на (рис. 1.11, б). 3. Определяем перемещения сечения К. Для этого используем интеграл Мора, формулы А.К. Верещагина, Симпсона, (см. раздел "Прямой изгиб”). Определяем вертикальное перемещение сечения К. Для этого освобождаем раму от всех внешних нагрузок (q, Р) и прикладываем в этом сечении единичную безразмерную силу (рис.1.13, а). Направление силы принимаем сами, например, в низ.

Расчет методом сил статически неопределимых систем, работающих на растяжение или сжатие

Рис. 1.13 На рис. 1.13, а представлена эпюра изгибающих моментов М1 от этой силы. Производим перемножение эпюр М и М1 по способу Верещагина, находим вертикальное перемещение сечения К. На участке 4-К использовалась формула Симпсона, а на участке 2-4 формула Верещагина. Определяем горизонтальное перемещение сечения К. Для этого раму освобождаем от внешних нагрузок, загружаем единичной безразмерной силой, приложенной горизонтально (рис.1.13, б). Эпюра от этой силы показана на рис. 1.13, б. Вычисляем горизонтальное перемещение, используя формулы Верещагина и Симпсона. Знак минус указывает, что действительное горизонтальное перемещение направлено в противоположенную сторону приложения единичной силы, т. е. влево. 15 Находим полное перемещение сечения К как геометрическую сумму найденных перемещений. Направление полного перемещения определяется углом (рис 1.14, б). Определяем угол поворота сечения К. Прикладываем в сечении К единичный безразмерный момент (рис.1.14, а) и строим от него эпюру изгибающих моментов.

Расчет статически неопределимых стержневых систем методом сил в матричной форме

Рис. 1.14 Производим перемножение эпюр М и М3, используя формулу Верещагина, находим угол поворота сечения К: 16 1.3. Расчет статически неопределимых стержневых систем методом сил Наиболее широко применяемым методом раскрытия статической неопределимости стержневых систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных (лишних) связей как внешних, так и внутренних, а их действие заменяется силами и моментами. Величина их в дальнейшем определяется так, чтобы перемещения соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом при указанном способе решения неизвестными оказываются силы или моменты, действующие в местах отброшенных или рассеченных связей. Отсюда и название «метод сил». Сущность метода сил рассмотрим на примере расчета статически неопределимой рамы, изображенной на рис. 1.15. Считаем, что внешняя нагрузка, размеры и жесткости стержней известны. Порядок расчета 2.1. Устанавливаем степень статической неопределимости, для чего используем выражение, где X – число неизвестных (имеется 5 внешних связей); Y – число независимых уравнений статики, которые можно составить для рассматриваемой системы. Для заданной рамы число неизвестных реакций равно пяти, а число независимых уравнений трем, так как система сил плоская и произвольно расположенная, поэтому Система два раза статически неопределима. 2.2. Преобразуем заданную систему в статически определимую, геометрически неизменяемую и эквивалентную заданной системе, т. е. образуем основную систему. Для этого удаляем лишние связи путем их отбрасывания или перерезания. На рис. 1.15 изображена основная система, полученная путем отбрасывания лишних опорных связей, а на рис. 1.16 основные системы образованы путем отбрасывания и перерезания связей. Например, (рис. 1.16, а) в опоре А отброшена горизонтальная связь и в опоре С перерезана связь, препятствующая повороту сечения. Таким образом, для каждой статически неопределимой стержневой системы можно Рис. 1.15 17 подобрать несколько вариантов основных систем (рис. 1.15, 1.16). Необходимо особо обратить внимание на то, что при образовании основной системы метода сил недопустимо введение новых связей. Желательно, чтобы основная система была рациональной, т. е. такой, для которой легче строить эпюры внутренних силовых факторов и объем вычислений был наименьшим. Такая система показана на рис. 1.15 (вариант I). Здесь нет необходимости определять опорные реакции, если строить эпюры со свободного (незакрепленного) конца рамы. Рис. 1.16 2.3. Образуем эквивалентную систему путем нагружения основной системы внешними силами и усилиями отброшенных (перерезанных) связей (рис. 1.17). Неизвестные силовые факторы будем обозначать символом Xi, где i – номер неизвестного. Если отброшенные связи запрещают линейные перемещения, то неизвестными являются силы, при запрете угловых смещений – моменты. Если же основная система была получена путем перерезания лишних связей, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям рассеченной системы в местах перерезания. В рассматриваемом примере X1 и X2 представляют собой вертикальную и горизонтальную составляющие реакции шарнирной опоры А. 2.4. Составляем канонические уравнения метода сил, которые выражают в математической форме записи условия эквивалентности основной и заданной систем. Иначе они выражают условия, обозначающие, что относительные перемещения по направлению удаленных лишних связей от совместного действия внешней нагрузки и неизвестных усилий должны быть равны нулю. Для эквивалентной системы рассматриваемого примера на основании принципа независимости действия сил и рис. 1.18 канонические уравнения запишутся в форме

К фермам с оговоркой можно отнести шпренгельные балки, представляющие собой комбинацию двух- или трёхпролётной неразрезной балки и подпружной тяги; они характерны для стальных и деревянных конструкций, с верхним поясом из неразрезного прокатного профиля (пиленые брусья или пакеты клееных досок). Также могут быть шпренгельные железобетонные фермы небольших пролётов.

Материал из Википедии - свободной энциклопедии

где 11 – относительное перемещение в основной системе по направлению лишней неизвестной X1, вызванное этим же усилием; 12 – относительное перемещение по направлению лишней неизвестной Х1, вызванное усилием X2; 1P – относительное перемещение по направлению действия неизвестной X1, вызванное заданной нагрузкой. Рис. 1.18 Физический смысл этих уравнений. Первое уравнение отрицает возможность вертикального перемещения опорного сечения А по направлению лишнего неизвестного X1 от совместного действия заданной нагрузки Р и полных значений неизвестных X1 и X2. Аналогичный смысл имеет и второе уравнение. В указанной форме (1.1) использование уравнений при инженерных расчетах затруднительно, поэтому преобразуем их к новому виду. С учетом того, что для линейных систем справедливо выражение можно записать: где 11 – относительное перемещение в основной системе по направлению действия силы X1 от действия силы X1 1 (рис. 1.19); 21 – относительное перемещение в основной системе по направлению действия силы X2 от действия силы X1 1. Здесь X1 и X2 – действительные значения реакций отброшенных связей. Тогда канонические уравнения метода сил (1.1) запишутся в виде По аналогии для n раз статически неопределимых систем канонические уравнения имеют вид Здесь коэффициенты с одинаковыми индексами называют главными, а называют побочными коэффициентами. Главные коэффициенты всегда положительны. Побочные коэффициенты могут быть положительными, отрицательными и равными нулю. 1P  – называются свободными или грузовыми коэффициентами. 2.5. Определяем коэффициенты канонических уравнений. Эти коэффициенты представляют собой перемещения точек системы в направлении отброшенных связей, следовательно, их можно найти посредством интеграла Мора: Порядок определения коэффициентов: Рис. 1.19 20 а) строим эпюры изгибающих моментов для основной системы от заданной внешней нагрузки P и от единичных усилий отброшенных связей X11 (рис. 1.20); Рис. 1.20 б) вычисляем коэффициенты канонических уравнений. Поскольку рассматриваемая система состоит только из прямолинейных стержней и жесткости стержней в пределах их длин постоянны, то вычисления интеграла Мора производим по способу А.К. Верещагина путем перемножения соответствующих эпюр с использованием формул Симпсона и трапеций: 2.6. Записываем систему канонических уравнений. После подстановки найденных коэффициентов в уравнение (1.3) получаем: Решаем систему уравнений и находим неизвестные усилия, кН: Примечание. Если знак усилия получился отрицательный, то это означает, что действительное усилие (реакция) направлено в противоположную строну, чем усилие Xi, принятое в эквивалентной системе. Таким образом, раскрывается статическая неопределимость системы. 2.7. Строим окончательные (действительные) эпюры внутренних силовых факторов для заданной системы. Построение эпюр можно выполнить двумя способами. Первый способ Загружаем основную систему заданной нагрузкой и найденными усилиями X1 и X2 (рис. 1.17), после чего строим эпюры М, Q, и N также, как для обычной статически определимой системы. Построенные таким способом эпюры показаны на рис. 1.21, где ординаты эпюры изгибающих моментов отложены со стороны растянутых волокон. Такой метод наиболее удобен для простых систем. Второй способ Вычисляем значения изгибающих моментов в любом (обычно характерном) сечении на основании принципа независимости действия сил по формуле 22 где k – номер сечения, для которого определяется значение изгибающего момента; n – степень статической неопределимости системы. Рис. 1.21 При этом, если найденное усилие Xi имеет отрицательный знак, то соответствующую эпюру Mi необходимо зеркально отобразить относительно осей стержней. При определении действительных значений изгибающих моментов ординаты моментов в расчетных сечениях берутся из эпюр M1, M2 и MP с учетом их знаков. Знаки моментов в рассматриваемом сечении определяются в зависимости от того, с какой стороны от базовой линии расположены ординаты моментов и от положения точки наблюдателя. В нашем случае принимаем, что точка наблюдателя расположена внутри контура, поэтому за положительные значения моментов принимаются моменты, которые вызывают в расчетном сечении растяжение внутренних волокон, а отрицательные – внешних волокон контура. Например, для сечения Д рамы получаем Аналогично и для других сечений. Окончательная эпюра изгибающих моментов для заданной системы показана на рис. 1.21, а. 23 2.8. Проводим деформационную проверку правильности построения действительной эпюры изгибающих моментов. Смысл деформационной проверки состоит в подтверждении отсутствия перемещений в основной системе в направлении отброшенных (перерезанных) связей при найденных значениях неизвестных усилий. Так, если неизвестные усилия найдены правильно, то для рассматриваемого примера должны удовлетворяться равенства: Если построить эпюру единичных моментов 2то проверку называют проверкой на групповое перемещение (рис. 1.22): Отсутствие перемещения подтверждает правильность решения задачи. Если выполненные расчеты не подтверждают отсутствие перемещений точек основной системы в направлении отброшенных связей, то для выявления ошибки расчета необходимо проверить правильность определения коэффициентов канонических уравнений по формуле При отсутствии равенства в этом уравнении выполняется построчная проверка коэффициентов канонических уравнений. Первая строка: . Если нет ошибки расчета в этой строке, то должно соблюдаться условие: Аналогично можно выполнить проверки 2-й и других строк. При выполнении указанных проверок следует проверить правильность расчета грузовых коэффициентов: 2.9. Строим эпюру поперечных сил Q по эпюре изгибающих моментов М путем последовательного вырезания стержней из заданной системы и рассмотрением их как шарнирно опертых статически определимых балок. По концам стержней прикладываем моменты, значения и направления которых выбираем из эпюры М в соответствующих сечениях. При наличии внешних сил прикладываем их на соответствующих участках. Определяем опорные реакции из условия статического равновесия и строим эпюру Q как обычно для статически определимых балок. Для заданной рамы (рис. 1.15) при построении эпюры поперечных сил для стойки вырезаем участок АВ и в сечении В прикладываем момент В 3 , 56 M P взятый из эпюры действительных моментов М (рис. 1.21, б). Определяем опорные реакции из рассмотрения равновесия 3 P и строим эпюру поперечных сил Q (рис. 1.23). Рис. 1.22 25 Аналогичным образом вырезаем горизонтальный стержень (ригель) ВС, рассматриваем его равновесие и строим эпюру Q для этого участка рамы (рис. 1.24). Переносим эпюры Q для отдельных стержней на задан ную систему. Окончательная эпюра поперечных сил для заданной рамы показана на рис 7.14, б. Построение эпюры поперечных сил по эпюре изгибающих моментов возможно и на основании дифференциальной зависимости: где α – угол наклона прямой, очерчивающей эпюру изгибающих моментов, к базовой линии (оси бруса). Поперечная сила считается положительной, если изгибающий момент возрастает в направлении оси. Для рассматриваемого примера: 2.10. Производим построение эпюры продольных сил N.
Рис. 7.16 Рис. 1.24 26 Для этого используем метод вырезания узлов (вырезаем только внеопорные узлы сечениями, бесконечно близкими к узлу) и рассматриваем их равновесие под действием внешней нагрузки (если такова приложена к узлам) и усилий в отброшенных (перерезанных) связях. Вырезаем узел В. Прикладываем к нему поперечные силы, взятые в соответствующих сечениях из эпюры Q (рис. 1.23, б). Узел должен находиться в равновесии (рис. 1.25) под действием поперечных и продольных сил (неизвестных). Определяем неизвестные продольные силы из условия статического равновесия. Эпюра продольных сил показана на рис. 1.23, в. 2.11. Проводим окончательную проверку правильности решения задачи. Система (рама), внеопорный узел или какая-нибудь часть системы должны находиться в равновесии под действием внешней нагрузки и усилий отброшенных (перерезанных) связей. Для заданного примера рассматриваем равновесие рамы, используя уравнения статики (рис. 1.26):

Условие равновесия выполняется. Примечания. 1. Если рама имеет несколько внеопорных узлов, то проверкой охватываются все узлы.

Библиографический список

Рис. 1.25 Рис. 1.26 27 2. При проверке равновесия внеопорного узла необходимо кроме внутренних усилий (M, Q, N), взятых в соответствующих сечениях, приложить еще внешние усилия (сосредоточенные силу и момент), если таковые приложены в узле. В нашем случае нагрузка в узле отсутствует.